Logistic Regression

In this post I investigate the machine learning algorithm known as logistic regression. Despite the name, this is actually a classification method. In other words, we are using our features $X$ to predict a categorical response variable $y$, which represents qualitative data: yes/no, good/bad, small/medium/large, etc. For simplicity, we are going to assume that $y$ may take on just two values, $0$ and $1$. We will discuss the more general question of what happens when there are $3$ or more categories involved at the end of the post.

Given a new data point $X = (x_1, x_2, ..., x_n)$, we want to determine whether to assign it the value $1$ or $0$. Instead of trying deal with the function $y = f(X)$ directly, logistic regression attempts to approximate $p = p(y=1 \vert X)$, the conditional probability that $y$ is $1$ given that $X$ take on the values $(x_1, x_2, ..., x_n)$. Then we may assign this data point the value of $1$ if we estimate a probability higher than $.5$, and the value $0$ otherwise. A benefit in using this probability function, rather than $f(X)$ directly, is that it takes its values on an interval, and thus we may apply calculus methods.

A first thought may be to approximate $p$ by a line, but there is an obvious issue with this: any non-horizontal line (and note that a horizontal line would not be a useful approximation) takes values from negative infinity to infinity, while we know that $p$ should only take values from 0 to 1.

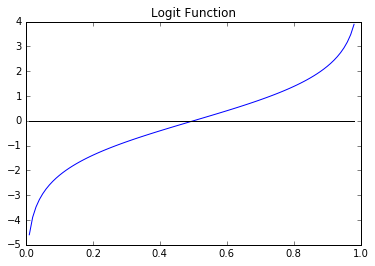
To fix this, note that $\displaystyle{\frac{x}{1-x}}$ takes the interval $(0, 1)$ to the positive real numbers $(0, \infty)$, and the natural logarithm $\text{ln}\,(x)$ takes the positive reals to the entire real line $(-\infty, \infty)$. Thus applying these functions in succession takes the open interval $(0, 1)$ to $(-\infty, \infty)$. This composition, $\text{ln}\,\displaystyle{\left( \frac{x}{1 - x}\right)}$, is called the $\textbf{logit}$ function, denoted $\text{logit}\,(x)$. The graph of the logit function looks like this:

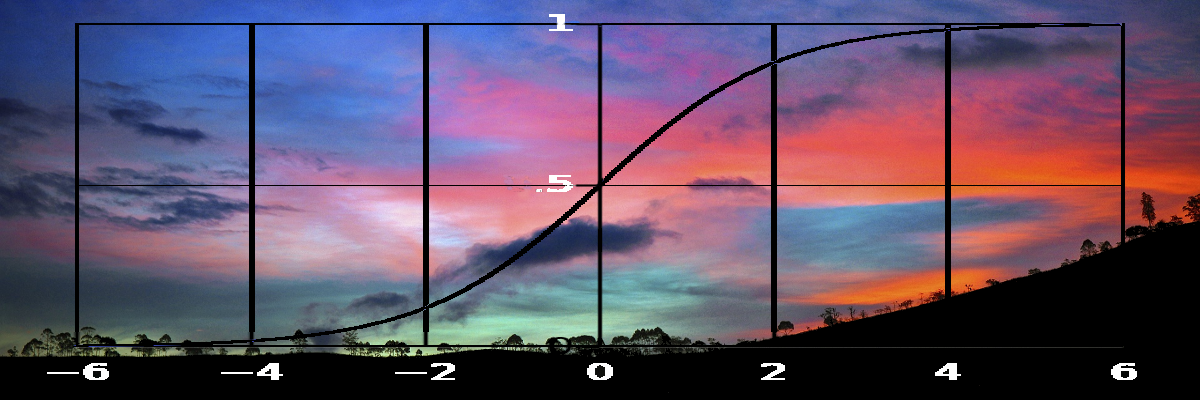
Also important to us is the inverse of the logit function, given by $\textbf{logit}^{-1}\,(x) = \displaystyle{\frac{1}{1 + e^{-x}}}$. This is called the $\textbf{logistic function}$, and its graph is called the S-curve:

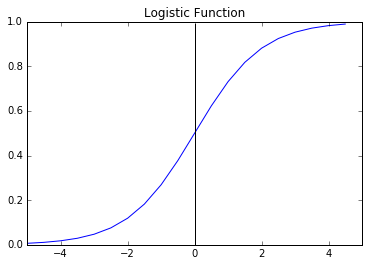
Our complaint about $p$ not being a good candidate for linear regression is no longer true after applying the logit function. The key idea behind logistic regression is that we can approximate $\text{logit}\,(p)$ by a linear function: \[ \text{logit}\,(p) \sim \beta_0 + \beta_1 \cdot X \] Applying the logistic function to both sides, we get the following approximation: \[ p \sim \displaystyle{\frac{1}{1 + e^{\, -(\beta_0 + \beta_1 \cdot X)}}} \]

The coefficients $\beta_0$ and $\beta_1$ can be found using maximum liklihood estimates (MLE), as we explain in that post, and this gives us our desired prediction.

Now suppose that the response variable $y$ takes $k$ possible values. Then for each $c \in \{ 0, 1, 2, ... , k-1 \}$ we can approximate $p^{(c)} = p(y = c \vert X)$ by: \[ p^{(c)} \sim \displaystyle{\frac{1}{1 + e^{\, -(\beta^{(c)}_0 + \beta^{(c)}_1 \cdot X)}}} \]

We then assign $y$ the value corresponding to the largest probability. Again, the $c\cdot k$ coefficients can be predicted using MLE.